Возможность точно предсказать результат взрыва до нажатия кнопки является основополагающей целью для многих взрывников по причине экологических и экономических ограничений нашего века.
Автор: доктор Тьери Бернард, компания TBT
Основываясь на фундаментальном механизме разрушения горных пород взрывчатыми веществами, на самых последних исследованиях в области цифрового моделирования, а также на мощности современных компьютеров и возможностях, предлагаемых беспилотными летательными аппаратами, мы разработали реалистичную цифровую имитационную 3D-модель для взрывов, проводимых на открытых и подземных горных работах. Этот новый тип модели позволяет нам одновременно моделировать фрагментацию породы, ее движение и связанные с ними сейсмические уровни, все в течение нескольких минут, что отлично укладывается в общий производственный цикл. В связи со сложностью модели в данной статье раскрываются основные принципы и сравниваются результаты моделирования с натурными измерениями в различных секторах, т. е. карьерах, шахтах и тоннелях.
Цифровое моделирование и эмпиризм
Метод проб и ошибок был основой прогресса и развития с давних времен. Горнодобывающий мир использовал этот эмпирический инструмент с самого начала для тестирования множества конфигураций заряда скважин и последовательностей инициации на основе многообразия рельефов поверхности взрывания. Сегодня мы знаем, что взрыв — это сложное физическое явление, которое приводит в динамическое взаимодействие механизмы детонации, механики, термодинамики и баллистики — мы перечисляем только наиболее очевидные. С каждым днем все сложнее совместить многофакторность взрыва, условия производства, ограничения безопасности и защиты окружающей среды — требования, которые накладываются на горнодобывающую промышленность 21-го века, с нынешним экономическим кризисом, жестокой конкуренцией между производителями, а также с необходимостью поддержания постоянного качества добываемого материала. Иногда даже запрещено прибегать к экспериментам на месте. Тем не менее в конечном итоге это позволит горнодобывающей промышленности повысить свою производительность, оптимизировать цену и предложение продукции с учетом конкуренции.
Цифровое моделирование (или цифровые эксперименты) позволяет нам воспроизвести сложное физическое явление на компьютере, развитие которого мы хотим изучить. Таким образом, цифровое моделирование позволило нам воспользоваться преимуществами процесса проб и ошибок, и одновременно — благодаря росту вычислительной мощности компьютеров — мы смогли включить в моделирование прогресс и знания, достигнутые в области физических явлений. Последнее невозможно было бы постичь с помощью традиционных экспериментальных методов.
Недетерминированный подход к цифровому моделированию взрывных работ
Кацабанис & Лю, Фавро, Прис и Чунг, Дэа-Брайан, Уэйд & Рэндалл в основном использовали детерминистские подходы из тесно связанных отраслей. В Европе Бернард использовал другой подход, основанный на его университетских исследованиях, проведенных в начале 1990-х годов, и разработал имитационную и так называемую целостную модель прогнозирования, основанную на детерминированных теориях.
Длительность решения детерминистических уравнений (академический подход) неприемлема для промышленности (цикл между двумя взрывами намного короче, чем время, необходимое для решения уравнений).
Поэтому доктор Бернард предложил прагматический подход, используя синтез детерминированных принципов, позволяющий набору идеально идентифицированных и известных причинных связей (например, физика Ньютона) работать вместе, чтобы решать проблемы и удовлетворять здесь и сейчас текущие потребности горнодобывающего сектора. Как только мы точно знаем структуру и тип элементов, которые мы хотим привести во взаимодействие, основная задача моделирования — попытаться имитировать реальность как можно ближе, точно воспроизводя каждый из ее механизмов.
Исчерпывающе смоделировать последовательность всех причин и вызванных последствий взрыва — это задача, которую самые сложные модели не смогли решить, несмотря на увеличение возможностей обработки, доступных физическим лицам и промышленному сектору. Не скрывая неполноту характера моделирования, разработчики программы I-Blast («Ай Бласт») прямо говорят о невозможности точного воспроизведения естественных механизмов в силу их большой сложности.
Верное и полное воспроизведение задействованных природных механизмов требует не только учета физико-химических характеристик взрывчатого вещества, совокупности геометрических параметров взрыва, положения скважин в пространстве и, конечно, последовательности инициирования, но и полного и обширного знания геологии и геомеханических свойств каждой из элементарных частиц породы. Еще несколько лет назад это казалось практически невозможным на современном уровне науки и техники, но сегодня это стало практически доступным и будет полностью таковым завтра.
Следовательно, цифровые вычисления используются для получения выражения, которое приближается к решению. Задействованные физические механизмы, хотя и дорогостоящие с точки зрения времени расчета, могут быть смоделированы за несколько часов или даже за несколько минут благодаря параллельным вычислениям на графических процессорах.
Целостный подход
Механизм фрагментации часто представлен как сложный механизм. Знание подмеханизмов, из которых он состоит, не может объяснить общий механизм.
Модель, представленная в настоящем документе, основана на целостном подходе к механизму фрагментации. Под целостностью мы понимаем общий подход к механизму с пониманием отдельных механизмов, из которых он состоит, и связей или взаимодействий, которые им управляют. Он состоит из модулей, называемых генами, которые описывают элементарный механизм с помощью уравнений физических принципов и диаграмм взаимодействия, соединяющих гены вместе, при необходимости с временным измерением, т. е. с учетом кинетики механизма или взаимодействия. Используются следующие физические принципы: термодинамика и детонация для расчета детонационного давления, механика горных пород, теория разрушения и распространения волн для создания трещин, фундаментальный принцип динамики и упругие удары для движущегося материала.
Принцип работы модели
При детонации заряда взрывчатого вещества в веществе происходят следующие явления (рис. 1):
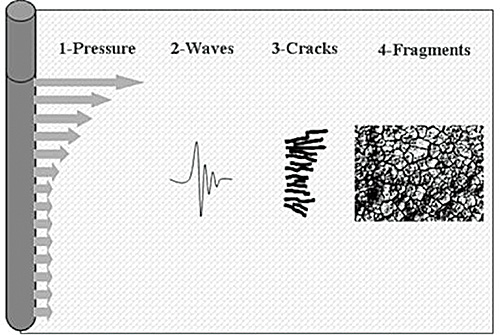
1) заряд взрывчатого вещества расщепляется с заданной скоростью на газ высокого давления и высокую температуру;
2) давление газа передается на забой скважины и создает поле напряжений в горной породе;
3) поле напряжений, из-за его импульсного аспекта, является источником Р-волны, которая перемещается в горной породе, повреждая ее;
4) поврежденные участки за пределами границ сжатия или растяжения породы являются центром образования трещин;
5) трещины распространяются со скоростью, присущей материалу, пока они не соединяются и не образуют сеть, которая определяет фрагменты;
6) давление газа уменьшается в сети трещин и отделяет фрагменты;
7) давление газа оказывается на грани фрагментов, создавая силы;
8) объединенные силы всех фрагментов производят ускорение и скорости выброса, которые передвигают фрагменты;
9) фрагменты двигаются по баллистической траектории и при этом касаются друг друга;
10) в тех областях, где повреждения недостаточно, чтобы вызвать трещину, P-волна напряжения продолжает свое путешествие, создавая вибрации.
Модель основана на генах (см. рис. 2), как объяснено выше, которые описывают элементарные механизмы фрагментации.
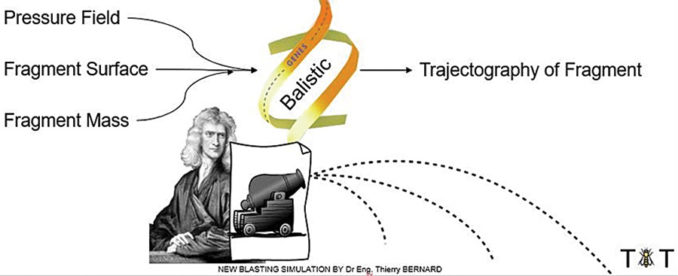
Наши современные знания физики, а также многочисленные публикации об этих механизмах позволяют нам построить следующее:
• ген «СкД», который определяет скорость детонации взрывчатого вещества в соответствии с его диаметром;
• «термодинамический» ген, который позволяет рассчитать детонационное давление заряда взрывчатого вещества с учетом диаметра отверстия;
• ген «давления», функция времени, которая обеспечивает детонационное давление за фронтом детонации;
• ген «Р-волны», который определяет распространение Р-волны, создаваемой сферическим источником давления;
• ген «стресс», который определяет поле давления, связанное с Р-волной;
• ген «разрушения», который определяет сос-тояние повреждения элемента породы, подвергнутого прохождению Р-волны;
• ген «трещины», который определяет распространение трещины внутри элемента материала;
• ген «фрагментации», который определяет размер фрагментов в элементе породы в соответствии с количеством трещин;
• ген «скорости выброса», который определяет начальный вектор скорости вокселя (воксель является эквивалентом в 3D пикселя в 2D; это элементарный объем материи) в зависимости от поля давления и динамической свободной поверхности;
• ген «свободной поверхности», который определяет границу между фрагментированными вокселями и интактными вокселями;
• «баллистический» ген, который определяет траекторию вокселя, подверженного воздействию поля давления;
• «ударный» ген, который определяет упругие ударные взаимодействия между двумя вокселями;
• ген «вибрации», который определяет сейсмическую амплитуду в вокселе в соответствии с интерференцией Р-волн.
О взаимодействии генов
Взрыв — это динамическое явление, которое начинается, когда взрывник нажимает кнопку, и заканчивается, когда осколки породы упали на землю и вибрации прекратились. Таким образом, это динамическое явление, которое учитывается в модели путем проведения ряда расчетов с интервалами. Для каждого временного интервала вычисляются гены, а также их взаимодействие. Конечное состояние предыдущего отрезка времени является начальным состоянием последующего.
Область взрыва моделируется с помощью трехмерной сетки пространства путем кубической дискретизации. Каждый куб (воксель) имеет механические характеристики породы, а также ряд определяемых признаков (например, минеральное содержание). Модель вокселя (см. рис. 3) определяется сетчатой поверхностью, созданной из облака точек, полученных в результате съемки местности, выполненной на месте с помощью 3D-сканера или беспилотного летательного аппарата.

Заряды взрывчатого вещества являются цилиндрическими и дискретизируются в элементарные сферические заряды с диаметром, равным диаметру скважины, причем каждая сфера является источником Р-волны.
Модуль фрагментации и перемещения
Когда мы изучаем эффекты P-волны в материале, самым простым подходом является рассмотрение аналогии волны, ударяющейся о стену на побережье. Волна повредит стену в самом слабом месте, и ущерб будет тем серьезнее:
• чем выше амплитуда волны;
• чем выше частота, с которой она бьется о стену;
• чем больше длина волны.
Мы разработали нашу модель повреждений, дублирующую этот механизм. Если нас интересует элементарный куб материала (воксель), то его можно различить макроскопически, используя модуль Юнга, коэффициент Пуассона, пределы прочности на сжатие и растяжение и скорость звука. Хотя повреждение представляет собой локальную декогезию слабого места в материале, его можно определить макроскопически как общее отношение максимальной положительной амплитуды Ac P-волны, деленной на предел сжатия ?lim _? (соответственно максимальная отрицательная амплитуда при делении на предел растяжения ?lim _?) для траектории P-волны от сферы взрывчатого вещества до свободной поверхности (см. таблица 2, левая сторона).
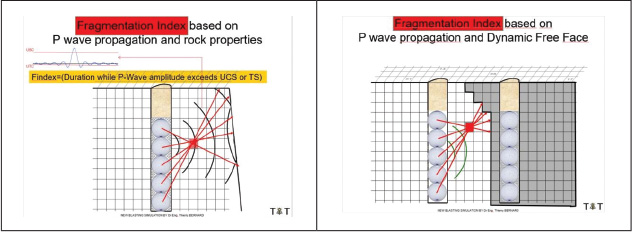

Свободная поверхность динамически определяется как предел между вокселями, которые не повреждены, и теми, которые фрагментированы и по которым трещины распространяются прямо (см. таблица 1, правая сторона).
Индекс повреждения определяется как общее отношение Ac/?lim _? или At/?lim _?. Когда это значение достигает 1, индекс фрагментации увеличивается на 1, а индекс повреждения возвращается к нулю. (Следует отметить, что этот метод позволяет нам начать моделирование со значением индекса повреждения или фрагментации, которое не равно нулю и которое соответствует естественному разрушению породы.)
Индекс фрагментации представляет собой количество слабых мест вокселя и будет связан с количеством трещин в последнем. Следовательно, она будет обратно пропорциональна размеру фрагментов в рассматриваемом вокселе.
Скорость выброса вокселя рассчитывается по тому же механизму, что и для фрагментации. Каждый воксель получает скорости от всех сфер модели, которые уже взорвались. Это влияние сферы на воксель получено путем применения фундаментального принципа динамики к коническому объему вещества, определенному вокруг оси сферы/вокселя.
Последняя фаза моделирования — это расчет для приведения вокселей в движение. Все они приобрели скорость выброса, поэтому движутся по стандартной баллистической траектории объекта в земной системе отсчета. Взаимодействия между блоками рассчитываются на каждом временном отрезке с помощью закона упругого удара, учитывающего тангенциальное и нормальное взаимодействия.
Калибровка модели
Хотя модель основана на ряде физических принципов, из-за макроскопического подхода некоторых механизмов она не может воспроизвести абсолютно точную реальность без калибровки. Напомним, что калибровка состоит в корректировке некоторых параметров моделирования, чтобы результат последнего более точно соответствовал измерениям, проведенным для реального эталонного случая. После калибровки модели применяемые физические принципы гарантируют, что в будущем моделирование даст приемлемые результаты. Для данной модели калибровка осуществляется с помощью следующих средств:
1) скорость выброса свободной поверхности взрыва измеряется с помощью портативного радара;
2) форма развала определяется через облако точек;
3) необязательно: смещение некоторых точек измеряется с помощью соответствующей системы.
Цифровое моделирование
Представленная ниже модель основана на физических принципах, применяемых к элементам, полученным путем дискретизации трехмерного пространства. Принципы периодически обновляются в соответствии с временной дискретизацией.
Если мы посмотрим на модель в таблице 3, размер области взрыва составляет примерно 200×70×15 м. Если мы представим объем вокселями с 1×1×1 м, мы получим 210 тыс. вокселей. Отверстия имеют диаметр 311 мм и заряжены на 12 м, дискретизация заряда дает 39 сфер на отверстие, что для 178 отверстий дает 6 942 сферы. Поэтому для каждого временного интервала существуют 210 000 * 6 942 = 1 457 820 000 конфигураций для расчета. Каждая конфигурация группирует вместе несколько генов. Количество элементарных вычислений, которые предстоит выполнить, исчисляется десятками миллиардов. Только однократное использование комбинированных параллельных вычислений на CPU и GPU делает это возможным в приемлемое время. Для приведенного примера машины с процессором 8-го поколения I7 и графической платой Nvidia 1050 требуется следующее время для полного моделирования (см. таблицу 2):
Этапы моделирования

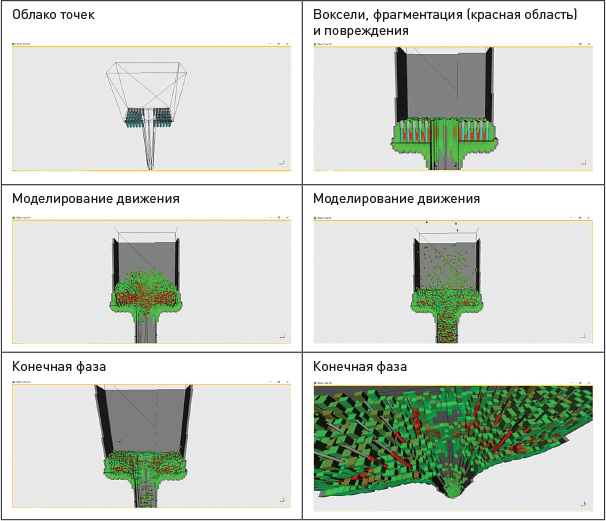
В таблице ниже приведены основные этапы моделирования для железорудного карьера с имитацией разубоживания.
Другой пример: туннель. Модель позволяет нам видеть вещи, которые мы не привыкли визуализировать.
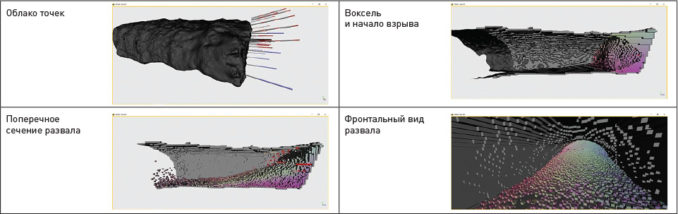
Другой пример: шахта. Создание взрывом камеры вокруг рудоспуска.
Результаты
Хотя цифровые значения являются конфиденциальными, результаты этих моделирований весьма обнадеживают, особенно после калибровки и для взрывов, контролируемых и выполняемых с электронным инициированием.
Действительно, для неконтролируемых взрывов со значительным вертикальным разбросом хаотический аспект проекций не учитывается моделью. Последнее дает локальные результаты, которые могут существенно отклоняться от реальности. Если макроскопическая тенденция правильна (расстояние разброса, площадь распространения фрагментов), то траектория отдельного вокселя может быть совершенно ошибочной. Аналогичным образом испытания, проведенные с вероятностными временами инициирования (типичными для пиротехнических детонаторов), показывают значительные вариации для вокселей, близких к начальным свободным поверхностям.
Вывод
«Реалистичное» 3D-моделирование, т. е. показ фрагментации и движения материала во время взрыва, стало возможным главным образом благодаря наличию параллельных вычислений на портативных компьютерах. Технология также помогла получить точные данные о горных породах, такие как поверхность местности с помощью беспилотных летательных аппаратов, и геологии с помощью непрерывных измерений во время бурения.
Через 10–15 минут результаты моделирования доступны, что делает инструмент пригодным для ежедневного использования, следовательно, для производства, главным образом для контролируемых взрывов, инициируемых электронными детонаторами.
Область применения разнообразна: поверхностные взрывы, подземные, специальные взрывы и т. д. Они позволяют либо проверить параметры и оценить их последствия, такие как распространение развала, разрушение целиков или разубоживание, либо они позволяют нам изучить внутреннее поведение взрыва и, следовательно, лучше понять его.
В недалеком будущем, поскольку вычислительная мощность постоянно растет, этот тип моделирования должен быть способен выполняться почти в режиме реального времени, одновременно с получением данных.
Спасибо!
Автор благодарит горнодобывающие компании, которые доверили использовать эту модель в своей деятельности и позволили ее проверить.
Литература:
1. Bernard, T., 1995. Maîtrise de l’énergie explosive. Action de l’explosif sur le milieu environnant. Thèse, Institut de Géodynamique URA-CNRS, Nice, France.
2. Bernard, T., 2010. «New blasting simulation approach», Fragblast — Proceedings of the 9th International Symposium on Rock Fragmentation by Blasting. Granada, Spain. Edition Sanchidrián, Taylor & Francis Group, Londres, R.U., pp. 437–446.
3. Bernard,/ Dozolme, 2013, 2nd International Symposium on Innovation and Technology in the Phosphate Industry. La Simulation Numérique Des Sautages: un Enjeu Majeur Pour Les Exploitations Minières Au 21ème Siècle, , Agadir, Maroc.
4. Dare-Bryan, Peter (primary); Wade, Lindsay 2001, COMPUTER MODELLING OF BENCH BLASTING FOR GRADE CONTROL, Annual Symposium on Explosives and Blasting Research (International Society of Explosives Engineers: Cleveland).
5. Favreau, R. F.: «Blasting Simulation — Present and Future», CIM Annual Meeting,Ottawa, 1984.
6. Liu, L. and Katsabanis, 1995, RD.: «A Constitutive Model for Predicting Rock Fragmentation by Blasting», 1995 APS Topical Conference «Shock Compression of Condensed Matter»,Aug., 13–18,, Seattle, Washington.
7. Poincaré, H., 1908. Science et méthode. Edition Ernest Flammarion, Paris, France, p. 69.
8. Preece, D S, 1988. A spherical element mesh generator using a scanline technique, in Proceedings Eighth Biennial CUBE Symposium,18 p (Sandia National Laboratories: Albuquerque).
9. Preece, D S, 1993. Momentum transfer from flowing explosive gases to spherical particles during computer simulation of blastinginduced rock motion, in Proceedings Ninth Annual Symposium on Explosives and Blasting Research, pp 21–29 (International Society of Explosives Engineers: Cleveland).
10. D S Preece, A Tawadrous, S A Silling and B Wheeler4, 2016, Modelling Full-scale Blast Heave with Three-dimensional Distinct Elements and Parallel Processing D S Preece1 , A Tawadrous2 , S A Silling3 and B Wheeler4, in Proceedings Annual Symposium on Explosives and Blasting Research (International Society of Explosives Engineers: Cleveland).


