Мальцев Евгений Николаевич, главный специалист ООО «НИИПИ ТОМС» (Институт ТОМС)
Статья посвящена исследованию новых возможностей пространственной трехмерной интерполяции методами машинного обучения для решения традиционных геологических задач с недостатком данных. Впечатляющий успех моделей машинного обучения определяется богатыми возможностями и простотой в использовании, позволяющими воспроизводить чрезвычайно сложные зависимости за счет способности самообучаться. Оператор-специалист подбирает представительные данные, а затем запускает алгоритм обучения, который автоматически воспринимает и анализирует структуру входных и целевых данных. Модель, натренированная на ограниченном множестве данных, способна обобщать полученную информацию и показывать хорошие результаты на данных, не использовавшихся в процессе обучения. При этом от пользователя, конечно, требуется какой-то набор знаний о том, как следует отбирать и подготавливать данные, выбирать нужный алгоритм и интерпретировать результаты, однако уровень знаний, необходимый для успешного применения машинного обучения, гораздо скромнее, чем, например, при использовании геостатистических методов.
Перед тем как продемонстрировать построения интерполяционной модели содержаний металла на реальном примере создания блочной модели запасов одной из залежей золотосеребряных руд (Практический пример 2), у автора возникла идея, условно говоря, протестировать сам аналитический и методический подход, лежащий в основе машинного обучения, показав его максимально практично, на простом математическом примере (Практический пример 1).
Практический пример 1
Предположим, что у нас есть Обучающая выборка, представляющая собой матрицу (или, проще говоря, Таблицу данных), которая имеет три столбика случайных переменных значений a, b и с, сгенерированных в количестве 100 наблюдений для каждого из трех полей переменных (a, b и с) в диапазоне от 0 до 100. Далее для каждого из 100 наблюдений выполним простой расчет значений в новом поле Y по формуле: Y=2*a+3*b+5*c. Затем на данной Обучающей выборке «потренируем» алгоритмы машинного обучения в том, чтобы по значению входных переменных a, b и с предсказывать значение целевой переменной Y (смотри рис. 2). Особенность данного обучения состоит в том, что модель обучается на исходных входных и целевых данных, находит специфические связи, указывающие на зависимости внутри данных, и на их основе строит свой прогноз, при этом не зная о самой математической формуле, используемой нами при расчете целевой переменной Y. Выходные значения каждой итерации сравниваются с целевыми выходными значениями, которые также содержатся в наборе исходных данных, и ошибка, т. е. разность между желаемым и реальным выходом, используется для корректировки весов сети так, чтобы уменьшить эту ошибку.
Качество предсказания целевой переменной Y оценивается по двум основным показателям: Rsquared — коэффициент детерминации (квадрат коэффициента линейной корреляции) и RMSE — среднеквадратичная ошибка (ошибка прогнозирования) — это часто используемая мера различий между значениями. Показатели качества предсказания несколькими наилучшими методами для Обучающей выборки приведены в таблице 1.
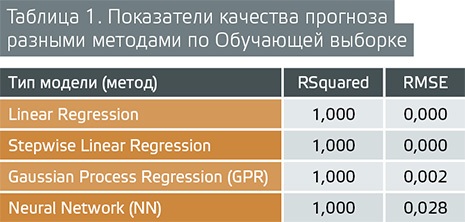
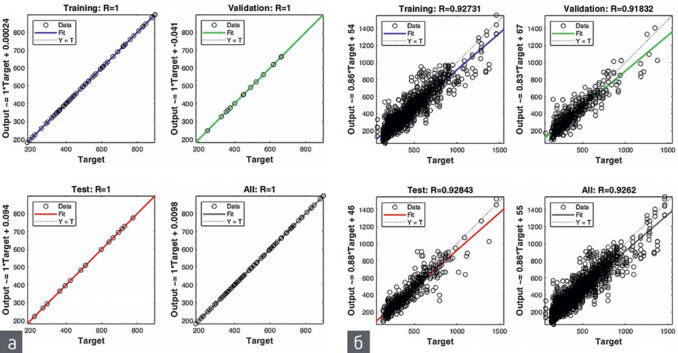
Единственная опасность, которой нужно остерегаться, — это переобучение модели, когда она просто «запоминает» примеры и плохо распознает любые другие примеры, не участвовавшие в процессе обучения (т. е. примеры, предъявляемые ей в процессе практического использования). Один из способов преодолеть проблему переобучения — разбить всю выборку на два или три подмножества: обучающую (Training), контрольную (Validation) и тестовую (Test). Эти случайные подвыборки используются для: 1) обучения, 2) проверки или контроля производительности сетей во время обучения и 3) итогового тестирования обученных моделей, чтобы определить, насколько хорошо модели работают на «новых» данных. Точность прогноза на трех случайных подвыборках и по всей Обучающей выборке показана на диаграммах рассеяния на рисунке 1.
На основе приведенных выше метрик можно сделать ВЫВОД № 1 о высоком качестве предсказания и сделать предположение о том, что обученные модели можно использовать для предсказания на последующей прогнозной выборке, т. е. точно прогнозировать значение Y на любом количестве новых вводных переменных a, b и с.
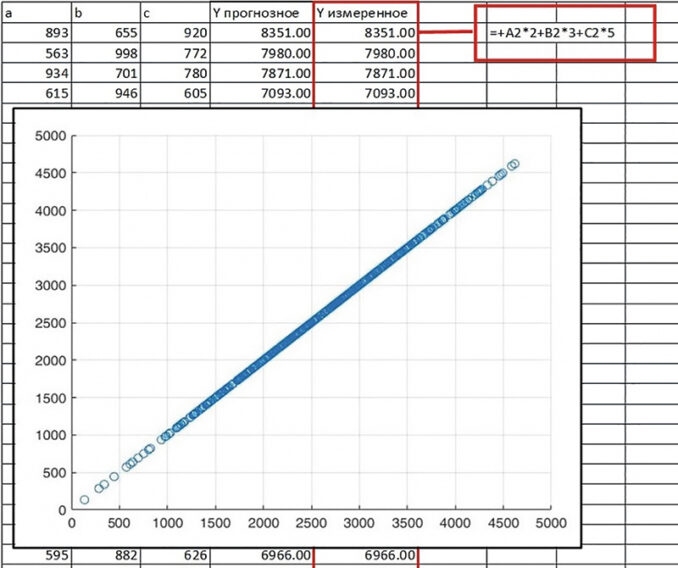
Для того чтобы проверить ВЫВОД № 1 (о высокой точности предсказания), создадим новую Таблицу данных, уже в качестве Прогнозной выборки, которая представляет собой три столбика случайных переменных значений a, b и с, сгенерированных в диапазоне от 0 до 500. Спрогнозируем четырьмя разными методами значение Y прогнозной, а затем рассчитаем Y измеренное по формуле: Y = 2*a+3*b+5*c в дополнительном контрольном столбике (для оценки качества прогноза). Таким образом, большая часть значений в Прогнозной выборке отличается от значений в Обучающей выборке, т. е. является совершенно новыми и неизвестными наблюдениями, не использовавшимися в процессе обучения для раннее натренированных (на 100 наблюдениях) моделей.
Качество предсказания целевой переменной Y прогнозное для выборки в количестве 500 наблюдений оценивалось четырьмя разными методами по показателям Rsquared (коэффициент детерминации) и на диаграммах рассеяния.
Практически идеальная корреляция измеренных данных и предсказанных значений для 500 наблюдений Прогнозной выборки, показанная на рисунке 2 (на примере метода GPR), доказывает высокую точность предсказания и истинность ВЫВОДА № 1.
Для справки: модели предсказания на основе машинного обучения тестировались также на прогнозных выборках в диапазонах 500–1 000 и 100–1 000 (в качестве дополнительных экспериментов), полностью новых, т. е. отличных от тех, что использовались при обучении моделей. Отмечено, что и на дополнительных прогнозных выборках (в диапазонах 500–1 000 и 100–1 000) высокая точность предсказаний оставалась неизменной.
После того как на моделях, которые отличаются очень четкой (на основе математического уравнения) зависимостью, была доказана высокая точность предсказания, далее, уже на реальных геологических данных рядового кернового опробования, можем исследовать точность алгоритмов машинного обучения для задач межскважинной интерполяции содержаний полезного компонента, которые заведомо отличаются менее четкой зависимостью между входными и целевыми переменными. Сравнить силу корреляционных зависимостей позволяют диаграммы рассеяния Обучающих выборок 1-го и 2-го примеров на рисунке 1.
Практический пример 2
Важно напомнить, что любой среднестатистический специалист по блочному моделированию, используя трехкратное или четырехкратное (а иногда и пятикратное) увеличение радиуса поискового эллипсоида, для того чтобы добиться полного заполнения блочной модели интерполированными значениями, наверняка задумывался о достоверности оценки содержаний, которая выполнена на таких больших расстояниях интерполяции. По мнению автора, для третьего поискового эллипсоида интерполяции берется трехкратный коэффициент расширения радиуса, а радиусы эллипсоида по соответствующим направлениям должны быть примерно в 1,5–2 раза больше, чем шаг наименее плотной разведочной сети в этом направлении. Дальнейшее (четвертое или пятое) увеличение радиуса поискового эллипсоида зачастую применяется, но при этом резко снижается достоверность использования и пригодность интерполятора IDW и/или кригинга. Кроме того, применение IDW и кригинга имеет ряд недостатков. Эти методы часто приводят к излишнему сглаживанию пространственного распределения исследуемых признаков в условиях дефицита данных и сильной анизотропии пространственного распределения признаков.
Таким образом, была поставлена задача построения трехмерной блочной модели запасов одной из залежей золотосеребряных руд методами машинного обучения, а именно: в качестве входных признаков использованы трехмерные координаты точки; в качестве целевой переменной — содержание серебра; алгоритмы машинного обучения — регрессия на основе Gaussian Process Regression (GPR) и k-Nearest Neighbors (k ближайших соседей, или, сокращенно, kNN); функционал качества прогноза — коэффициент линейной корреляции (R), коэффициент детерминации (RSquared) и относительная погрешность оценки среднего содержания серебра.
Gaussian Process Regression (GPR) — это регрессия гауссовского процесса, которая относится к классу случайных/стохастических процессов, определяющих значения случайных величин, на основе закономерностей распределения в пространстве.
Интерполяция на основе kNN — это один из часто используемых (наряду со стандартными методами «взвешивание обратного расстояния» (IDW) и «кригинг») алгоритмов пространственной интерполяции, который характеризуется улучшенным поиском ближайших соседей и взвешиванием.
По каждой из 28 разведочных линий все скважинные рудные подсечения были пронумерованы по направлению падения рудного тела в порядке возрастания глубины. Количество уникальных порядковых номеров скважин в линии составило от 3 до 12. Далее соответствующие трехмерные координаты точек в базе данных для машинного обучения были также прокодированы с помощью дополнительного поля «ЧетНечет» соответствующими порядковыми номерами по направлению падения рудного тела. Выборка нечетных (или четных) порядковых номеров позволила, таким образом, создать на основе изначальной детальной разведочной сети 20 × 20 м новую разряженную сеть скважин с шагом 40 × 40 м. Основная идея эксперимента в том, что четные номера устраняются из процедуры «обучения» (Обучающая выборка — сеть 40 × 40 м), а потом возвращаются для проверки точности прогноза уже по всем — и четным, и нечетным — вместе (Прогнозная выборка — сеть 20 × 20 м). Процесс оценки представляет собой сравнение оцененных значений с действительными известными значениями в узлах интерполяции. Особенность эксперимента заключается в том, что Прогнозная выборка одновременно является еще и контрольной, т. к. мы знаем и «четные», и «нечетные» содержания серебра.
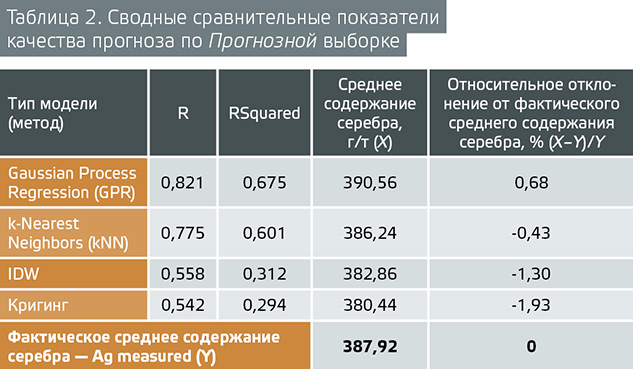
В таблице 2 приведены сводные сравнительные показатели качества прогноза:
• коэффициент линейной корреляции R,
• коэффициент детерминации RSquared,
• сопоставление результатов оценки среднего содержания серебра разными методами.
В сравнении участвовали два метода машинного обучения — GPR и kNN, а также два стандартных метода интерполяции — IDW и кригинг.
Результаты сравнения доказывают ВЫВОД № 2 о том, что разработанные методы межскважинной интерполяции на основе алгоритма машинного обучения отличаются большей точностью, чем стандартные методы интерполяции IDW и кригинг.
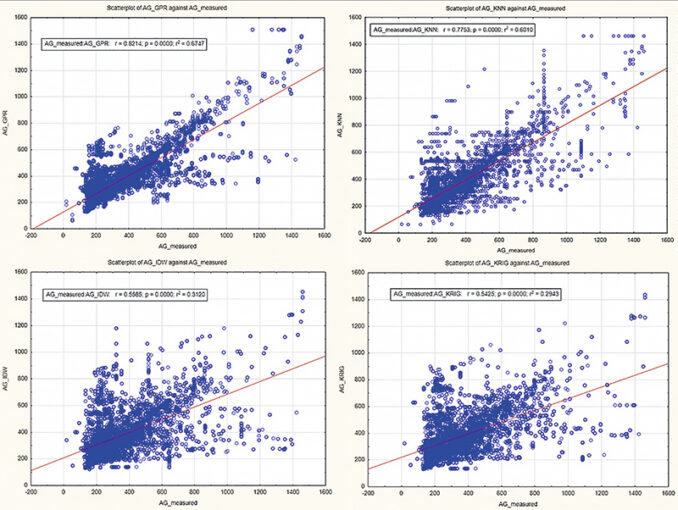
Точность прогноза также оценивалась визуально-графическим способом на диаграммах рассеяния на рисунке 3. Анализируя представленные графики, можно сделать вывод о том, что более «плотным» распределением точек выделяется метод GPR, что говорит о лучшей сходимости результатов.
Заключение
Подводя итог, можно сделать окончательный вывод о высокой (точность — 82 %) эффективности применения методов машинного обучения для задач межскважинной интерполяции, что являлось основной целью данного исследования.
Таким образом, блочное моделирование на основе машинного обучения имеет следующие преимущества:
• Получаемый результат более точно соответствуют исходным данным.
• Многовариантное моделирование, за счет создания нескольких реализаций (версий), каждая из которых моделирует геологическую обстановку, выделяя более и менее точные реализации.
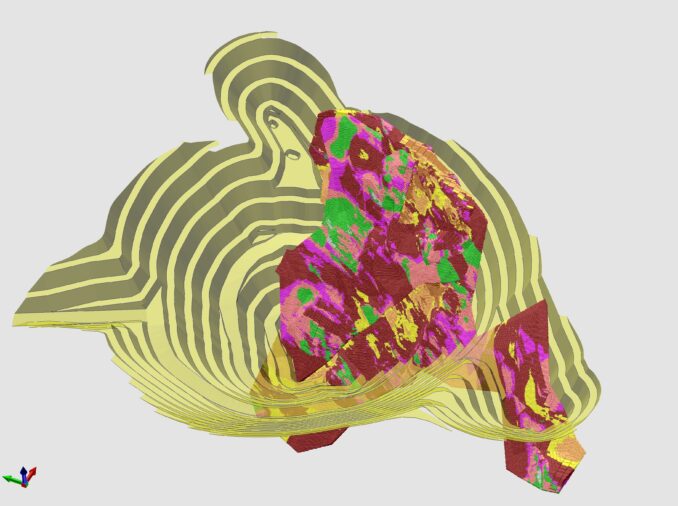
• Возможность получить достаточно контрастное изображение неоднородных областей, что позволяет выделить неоднородности, чьи геометрические размеры меньше расстояния между скважинами.
• Методика проста в настройках и управлении. Способности моделей к самообучению позволяют находить закономерности в исходных данных. Не требует от геолога знаний нюансов геостатистики.
• Возможность быстрого выполнения кросс-валидации (в отличие от стандартных методов интерполяции — IDW и кригинг). Следовательно, более быстрый способ обучения данных, при этом избегая переобучения.
• Скорость работы выше, чем у традиционных алгоритмов.
• Повышение достоверности оценки показателей руды как альтернатива использованию больших радиусов поискового эллипсоида в условиях недостатка исходных данных.
Полученные решения имеют большие потенциальные возможности для дальнейшего совершенствования. В частности, в последующих исследованиях планируется разработать на основе имеющейся методики новый подход выделения рудных тел без необходимости каркасного моделирования, на основе только лишь исходных данных и с учетом априорной геологической информации (направления падения и простирания тела).
Эти методы могут быть успешно использованы для обучения алгоритма с целью последующего прогноза значений исследуемых параметров на неразбуренных участках (в точках с отсутствующей информацией), с последующей оценкой качества и устойчивости прогнозной способности методов и алгоритмов.